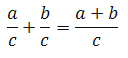sábado, 27 de febrero de 2010

Los Números Racionales (Q)


Número racional es un cociente de dos enteros, con denominador distinto de cero.
Se representa por Q.

Son números racionales

Fracciones 2/3, -5/7
Decimales finitos 2,4; -3,66
Los enteros cuyo denominador es el 1, el que no se escribe. Por lo tanto, el conjunto Q de los racionales tiene subconjunto a los enteros (Z).



Representación gráfica de Q.
Los números racionales se representan con puntos sobre una recta tomando una unidad arbitraria y representando primero a los enteros. Los racionales o fracciones serán puntos como ½ (punto medio del segmento 0, 1); 1/3 (tercio del mismo segmento); etc.
El conjunto Q es denso porque entre dos números racionales siempre existe otro.


Suma y diferencia de números racionales

  • Con el mismo denominador. Se suman los numeradores y se mantiene el denominador.


  • Con distinto denominador. Se reducen los denominadores a común denominador, y se suman los numeradores de las fracciones equivalentes obtenidas



Propiedades de la Suma y resta de números Racionales.

1. Interna: La suma resta de números racionales da otro racional.
2. Asociativa: Al agrupar los sumando no varía el resultado.
3. Conmutativa: El orden de los sumando no varía la suma.
4. Elemento neutro: El cero. A todo número que se le sume cero da el mismo número.
5. Elemento Opuesto: A todo numero racional que se le sume su opuesto da como resultado cero.

Producto de los números Racionales
El producto de dos números racionales da otro racional, que tendrá por numerador el producto de sus numeradores y por denominador el producto de su denominadores.

Propiedades de productos de los números racionales

1. Interna: El producto de números racionales da otro racional.
2. Asociativa: Al agrupar los factores no varía el resultado.
3. Conmutativa: El orden de los factores no varía el producto.
4. Elemento neutro: El uno. A todo número que se le multiplique por uno da el mismo número.
5. Elemento inverso: A todo numero racional que se multiplique por su inverso da como resultado uno.
6. Distributiva con respecto a la suma.

Cociente de los números racionales
El cociente de dos números racionales da otro racional, que tendrá por numerador el producto de los extremos y por denominador el producto de los medios.

Potencia de un número racional
Si un número racional Q se encuentra elevado a una potencia n que pertenece a z, se elevara el numerador y el denominador a dicha potencia, de forma distributiva.

Propiedades de las potencias de fracciones
Publicado por en No hay comentarios:

jueves, 18 de febrero de 2010

Los Números enteros (Z)


El sistema numérico de los números naturales quedaba limitado, ya que no nos permitía ciertas operaciones representativas, como por ejemplo, una deuda, una temperatura bajo cero o un saldo en contra. Para solucionar esta deficiencia se crean los números enteros, mismos que pueden ser positivos o negativos.



El conjunto de los enteros se representa

Z= {...,-4,-3,-2,-1, 0, 1, 2, 3,4,...}

Representación en la recta:


Se considera a los números naturales un subconjunto de los enteros.

El valor absoluto de un número entero

Es el número natural que resulta de “quitar” el signo + ó ‒ que le precede. El valor absoluto representa la distancia del cero a dicho número.
Se representa el número entre barras:


Opuesto de un número entero
Es el que tiene el mismo valor absoluto y distinto signo.

op(-4)= +4
op(-6)= +6
op(+2)= -2
op(0)=0


Comparación de números enteros
Un número a diremos que es menor que b si a está situado a la izquierda de b:
Utilizaremos los símbolos < y > (menor que y mayor que)
-3< 2                    3 < 4                 -4<-2

Operaciones con números enteros

Suma y resta de números enteros
1) Cuando los números enteros tienen el mismo signo se suman y el resultado queda con el mismo que tienen los números que sumé.
3 + 5 = 8              - 3 - 5 = - 8

2) Cuando los números tienen distintos signos resto el valor absoluto del mayor al valor absoluto menor y el resultado da con el signo del valor absoluto del mayor.
- 5 + 2 = -3             5 - 2 = 3


Propiedades de la suma de los números enteros
La suma tiene cuatro propiedades. :
Conmutativa, asociativa, distributiva y elemento neutro.

Propiedad conmutativa: El orden de los sumandos no altera el resultado
a + b = b + a

Propiedad asociativa: Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman.
(a + b) + c = a + (b + c)

Propiedad distributiva: La suma de dos números por otro número es igual a la suma de cada sumando multiplicado por ese otro número.
a . (b + c) = a.b + a.c

Elemento neutro: El cero sumado a cualquier número da el mismo número.

a + 0 = a


Multiplicación de números enteros
Para multiplicar dos números enteros, se multiplican sus valores absolutos y el signo se obtiene utilizando la Regla de los signos, que dice lo siguiente:

Ejemplo

(+4) • (+2) = +8
(-4) • (-5) = +20
(+5) • (-7) = -35
(-1) • (+5) = -5

Propiedades de la multiplicación
Las propiedades conmutativa, asociativa, elemento neutro y distributiva.

Propiedad conmutativa: El orden de los factores no altera el producto.
a . b = b . a

Propiedad asociativa: Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman.
(a . b) . c = a . (b . c)

Propiedad de elemento neutro: cualquier número multiplicado por uno es el mismo número.
 a . 1 = a

Propiedad distributiva. Con respecto a la suma.

a . (b + c) = a.b + a.c

División de números enteros
Para dividir dos números enteros, se dividen sus valores absolutos y se pone el signo que se obtiene con la Regla de los Signos.





Potencia con números enteros
Si el exponente es un número positivo (recordando que cuando no tiene signo es número positivo también), podemos afirmar que de acuerdo al signo de la base y si el exponente es número par o impar, tendremos:
Sea cualquier número entero y n el exponente entero también, tenemos:
Actividad interactiva clic en el siguiente link (auto-evaluación)
Valor absoluto y opuesto
Suma
Resta
Producto
División
Operaciones combinadas
Publicado por en No hay comentarios:

martes, 16 de febrero de 2010

Los Números Naturales (N)

Los números naturales surge en el comienzo de las distintas civilizaciones, por La necesidad del hombre de contar y de ordenar.
Los números naturales son ordinales, pues sirven para ordenar los elementos de un conjunto:
1º (primero), 2º (segundo),…, 6º (sexto),…

Las operaciones que se pueden realizar son:

• Suma y resta es una operación que se deriva de la operación de contar

• La Multiplicación es la suma sucesiva del mismo número.

• La división es la operación de repartir.


Estas operaciones pueden ser internas y no internas

Las internas: Operaciones que siempre da un número natural. Adición y multiplicación.

Las No internas: Operaciones que no siempre dan un número natural. La sustracción y la división

Con el número natural, se designa la cantidad de elementos que tiene un conjunto, llamándolo cardinal del conjunto.

El conjunto de todos ellos se designa por N:

N = {0, 1, 2, 3, 4,…, 145,146….}

Si al conjunto se le excluye el 0 designa por N*:

N* = {1, 2, 3, 4,…, 145,146….}

El conjunto de los números naturales es infinito y es el conjunto de los números más elemental.

Propiedades de la adición de Números Naturales

1.- Asociativa:Siendo a, b, c números naturales cualesquiera se cumple que:

(a + b) + c = a + (b + c)

Ejemplo:
(6 + 4) + 8 = 10 + 8 = 18
6 + (4 + 8) = 6 + 12 = 16
es decir,

(6 + 4) + 8 = 6 + (4 + 8)

2.-Conmutativa: Si a, b son números naturales cualesquiera se cumple que:

a + b = b + a

Ejemplo:
6 + 3 = 9
3 + 6 = 9
En particular, para los números 6 y 3, se verifica que:

6 + 3 = 3 + 6

3.- Elemento neutro: El 0 es el elemento neutro de la suma de enteros porque, cualquiera que sea el número natural a, se cumple que:
a + 0 = a

Propiedades de la Sustracción de Números Naturales
La sustracción, no es una operación interna en N, pues la diferencia de dos números naturales puede no ser un número natural (no lo es cuando el sustraendo es mayor que el minuendo). Por eso se crea el conjunto Z de los números enteros, en el que se puede restar un número de otro, cualesquiera que sean éstos.

Ejemplo:
Si tenemos 6 caramelos y los niños se comen 2 ¿cuántos caramelos quedan? 
Se pueden contar los caramelos o podemos decir que 6 - 2 = 4.

La resta consta de minuendo (los caramelos iniciales) y sustraendo (los caramelos que se comieron los niños).

No es una operación interna en N, pues la diferencia de dos números naturales puede no ser un número natural (no lo es cuando el sustraendo es mayor que el minuendo). El resultado de la operación pertenecería al conjunto de los enteros Z.

Propiedad de la resta:
La resta no es conmutativa (no es lo mismo a - b que b - a)



Propiedades de la Multiplicación de Números Naturales

1.-Asociativa: Si a, b, c son números naturales cualesquiera se cumple que:

(a • b) • c = a • (b • c)

Ejemplo:
(4 • 3) • 6 = 12 • 6 = 72
4 • (3 • 6) = 4 • 18 = 72
es decir,

(4 • 3) • 6 = 4 • (3 • 6)

2.- Conmutativa: Si a, b son números naturales cualesquiera se cumple que:

a • b = b • a

Ejemplo:
2 • 4 = 4 • 2 = 8

3.-Elemento neutro: El 1 es el elemento neutro de la multiplicación porque, cualquiera que sea el número natural a, se cumple que:
a • 1 = a

4.- Distributiva del producto respecto de la suma: Sea a, b, c números naturales cualesquiera se cumple que:

a • (b + c) = a • b + a • c

Ejemplo:
3 • (4 + 5) = 3 • 20 = 60
3 • 4 + 3 . 5 = 12 + 30 = 60
es decir,

3 • (4 + 5) = 3 • 4 + 3 . 5

Propiedades de la División de Números Naturales

La división, no es una operación interna en N. Los términos de la división se llaman dividendo (lo que se divide), divisor (en cuento se divide), cociente (el numero al que queda dividido) y resto (lo que sobra).
La división se llama exacta si el resto es cero, su cociente da un número natural N y en caso contrario inexacta, el resultado estás dentro del conjunto Q.

Propiedad de la división
La división no tiene la propiedad conmutativa. No es lo mismo a/b que b/a.



Resumen en el video


Actividad interactiva haz clic en el siguiente link (autoevaluación)

http://www.ematematicas.net/naturales.php
Naturales
• Orden
• Suma
• Resta
• Producto
• Cociente
• Operaciones combinadas

Publicado por en No hay comentarios:

¿Qué es la Aritmética?

La aritmética es la parte de la matemática que estudia los números.


La palabra viene del griego antiguo (arithmetikós ),

La Aritmética estudia las propiedades de los números naturales y se extiende a clases cada vez más amplia de los números..

                                      La palabra aritmética significa arte de calcular
Los Números naturales se fundamenta mediante el método axiomático, o bien partiendo de concepto intuitivo de conjunto, haciendo corresponder a cada grupo de conjuntos coordinables un ente llamado número cardinal.

El Conjunto de los Números

Publicado por en No hay comentarios:
Suscribirse a: Entradas (Atom)