Aritmética: Los Números enteros (Z)

El sistema numérico de los números naturales quedaba limitado, ya que no nos permitía ciertas operaciones representativas, como por ejemplo, una deuda, una temperatura bajo cero o un saldo en contra. Para solucionar esta deficiencia se crean los números enteros, mismos que pueden ser positivos o negativos.

El conjunto de los enteros se representa

Z= {...,-4,-3,-2,-1, 0, 1, 2, 3,4,...}

Representación en la recta:

Se considera a los números naturales un subconjunto de los enteros.

El valor absoluto de un número entero

Es el número natural que resulta de “quitar” el signo + ó ‒ que le precede. El valor absoluto representa la distancia del cero a dicho número.

Se representa el número entre barras:

Opuesto de un número entero
Es el que tiene el mismo valor absoluto y distinto signo.

op(-4)= +4
op(-6)= +6
op(+2)= -2
op(0)=0

Comparación de números enteros

Un número a diremos que es menor que b si a está situado a la izquierda de b:

Utilizaremos los símbolos < y > (menor que y mayor que)

-3< 2 3 < 4 -4<-2

Operaciones con números enteros

Suma y resta de números enteros

1) Cuando los números enteros tienen el mismo signo se suman y el resultado queda con el mismo que tienen los números que sumé.

3 + 5 = 8 - 3 - 5 = - 8

2) Cuando los números tienen distintos signos resto el valor absoluto del mayor al valor absoluto menor y el resultado da con el signo del valor absoluto del mayor.

- 5 + 2 = -3 5 - 2 = 3

Propiedades de la suma de los números enteros

La suma tiene cuatro propiedades. :

Conmutativa, asociativa, distributiva y elemento neutro.

Propiedad conmutativa: El orden de los sumandos no altera el resultado

a + b = b + a

Propiedad asociativa: Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman.

(a + b) + c = a + (b + c)

Propiedad distributiva: La suma de dos números por otro número es igual a la suma de cada sumando multiplicado por ese otro número.

a . (b + c) = a.b + a.c

Elemento neutro: El cero sumado a cualquier número da el mismo número.

a + 0 = a

Multiplicación de números enteros

Para multiplicar dos números enteros, se multiplican sus valores absolutos y el signo se obtiene utilizando la Regla de los signos, que dice lo siguiente:

Ejemplo

(+4) • (+2) = +8

(-4) • (-5) = +20

(+5) • (-7) = -35

(-1) • (+5) = -5

Propiedades de la multiplicación
Las propiedades conmutativa, asociativa, elemento neutro y distributiva.

Propiedad conmutativa: El orden de los factores no altera el producto.

a . b = b . a

Propiedad asociativa: Cuando se suman tres o más números, el resultado es el mismo independientemente del orden en que se suman.

(a . b) . c = a . (b . c)

Propiedad de elemento neutro: cualquier número multiplicado por uno es el mismo número.

a . 1 = a

Propiedad distributiva. Con respecto a la suma.

a . (b + c) = a.b + a.c

División de números enteros

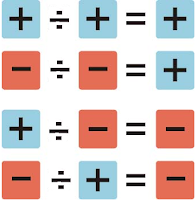
Para dividir dos números enteros, se dividen sus valores absolutos y se pone el signo que se obtiene con la Regla de los Signos.

Potencia con números enteros

Si el exponente es un número positivo (recordando que cuando no tiene signo es número positivo también), podemos afirmar que de acuerdo al signo de la base y si el exponente es número par o impar, tendremos:

Sea cualquier número entero y n el exponente entero también, tenemos: