Los números decimales
Los decimales son una forma de escribir números fraccionarios, sin escribir una fracción teniendo un numerador y un denominador.
La fracción 5/10 se podría escribir en forma decimal como 0,5
La coma decimal indica que este es un decimal.
El decimal 0,5 se podría decir como cinco décimos o como cero coma cinco.
Concepto de números decimal
Hacer clic en el siguiente link
Los números decimales son aquello que poseen una parte entera y una parte decimal separado por una coma.
Tipos de números decimales
Ejemplo de decimal exacto
0,342 → Parte decimal limitada. Decimal exacto.
Ejemplo de decimal No exacto
5,2323... → Parte decimal ilimitada. Decimal no exacto. Se repite la cifra
π=3,1415926... → Parte decimal ilimitada. Decimal no exacto. No se repiten cifras..
Ejemplo de decimal No exacto. Periódico Puro
Ejemplo de decimal No exacto. Periódico Mixto
Fracción Generatriz
Fracción generatriz: Es aquella fracción que genera al número decimal ósea la fracción irreducible que representa a un número decimal
Los números decimales exactos y periódicos puros y mixtos se pueden expresar en forma de fracción, hallando su fracción generatriz
Pasar de decimal a fracción generatriz
- De decimal Exacto a fracción generatriz. (Decimales finitos)
Numerador: debe tomarse el número completo sin la coma.
Denominador: el número 1 seguido de tantos ceros como decimales posea el número
Luego si es simplificable, se simplifica para obtener la mínima expresión de la fracción así como en el ejemplo b que se da a continuación
- De decimal NO exacto a fracción generatriz.
1) Decimales periódicos
Numerador: debe tomarse como número entero, ignorando la coma, restándole la parte no-periódica
Denominador: corresponde a tantos 9 como posea el periodo
Ejemplo
2) Decimales Semiperiódicos:
Numerador : debe tomarse como número entero, ignorando la coma, restándole la parte no-periódica
Denominador: tantos 9 como cifras del periodo, seguido de tantos ceros como cifras del antiperiodo.Debe tomarse la parte decimal y restarle la parte finita del número y luego dividir el resultado por tantos 9 como dígitos posea el periodo, seguido de tantos ceros como dígitos posea la parte finita.
Ejemplo
Los números Irraccionales
Los números irracionales son números decimales con un número ilimitado de cifras decimales no periódicas que no se pueden expresar en forma de fracción.
Los números irracionales más utilizados en Matemáticas son:
π (se lee pi), π =3,14159265358979...
Es la relación entre la longitud L de la circunferencia y su diámetro D
Para los cálculos con el número π se hace tomando un redondeo del mismo. 3,14
El número de Euler e = 2,7182818284...
En Economía, para predecir lo que genera un modelo económico
En Biología, para explicar el crecimiento de poblaciones y en la datación de fósiles.
Sanidad, para estudiar y evaluar enfermedades epidémicas.
El número áureo Φ (se lee fi), Φ =1,6180339887...
El número de Oro
Este número era utilizado por los griegos en las proporciones de sus construcciones. Y hoy día Se sigue utilizando en la concepción y diseño de cantidades de objetos, elementos arquitectónicos y artísticos.
Las raices inexactas como la √2=1,414213562….., entre otros.
"El conjunto de los Irraccionales, a diferencia del conjunto de los raccionales, no se pueden expresar mediante fracciones"
"La unión del conjunto de los raccionales con los irraccionales comforman el conjunto de todos los reales"
Reglas de Aproximación
Para aproximar números decimales, debemos tener en cuenta el primer dígito que se descarta:
• Si es igual o mayor que 5, se aumenta en una unidad el dígito anterior
• Si es menor que 5 se deja el dígito anterior
Hacer clic en los siguientes link para ejercicios interactivos
http://www.gobiernodecanarias.org/medusa/contenidos/recursos/teleformacion_final/AntRguez/act_12.htm






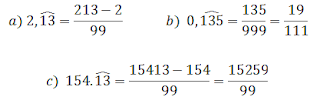


No hay comentarios:
Publicar un comentario